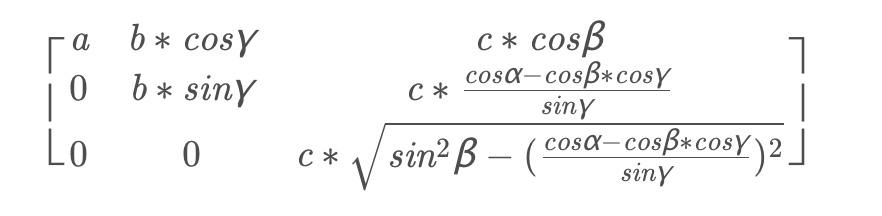最近在研究原子坐标变换的时候用到了两个矩阵,就记录一下。
- 绕转
import numpy as np
# 需要使用4 x 1的齐次坐标系,所以要把三维列补上一行(见第二句)
# theta: 绕转角;u,v,w: 归一化的绕转向量(旋转平面法向量,通过np.cross()获得)
rotationMatrix = np.array([[np.square(u)+(1-np.square(u))*np.cos(theta),u*v*(1-np.cos(theta))-w*np.sin(theta),u*w*(1-np.cos(theta))+v*np.sin(theta),0],
[u*v*(1-np.cos(theta))+w*np.sin(theta),np.square(v)+(1-np.square(v))*np.cos(theta),v*w*(1-np.cos(theta))-u*np.sin(theta),0],
[u*w*(1-np.cos(theta))-v*np.sin(theta),v*w*(1-np.cos(theta))+u*np.sin(theta),np.square(w)+(1-np.square(w))*np.cos(theta),0],
[0,0,0,1]])
coordinationMatrix_added = np.r_[coordinationMatrix,np.array([[1]])]
newCoordMatrix = np.dot(rotationMartix, coordinationMatrix_added)
- 相对坐标与绝对坐标变换
import numpy as np
# oldCoordinate: oldX, oldY, oldZ
# newCoordinate: newX, newY, newZ
# a, b, c
# alpha, beta, gamma
conversionMatrix = np.array([[a, b * np.cos(gamma), c * np.cos(beta)],
[0, b * np.sin(gamma), c * (np.cos(alpha) - np.cos(beta) * np.cos(gamma)) / np.sin(gamma)],
[0, 0, c * np.sqrt(np.sin(beta) * np.sin(beta) - np.power(
(np.cos(alpha) - np.cos(beta) * np.cos(gamma)) / np.sin(gamma), 2))]])